Basics of Combinatorics

Counting the objects that satisfy some criteria is a very common task in both Programming and in real-life situations. The myriad ways of counting the number of elements in a set is one of the main tasks in combinatorics, and I’ll try to describe some basic aspects of it in this blog.

Combinatorics is all about number of ways of choosing some objects out of a collection and/or number of ways of their arrangement. For example suppose there are five members in a club, let's say there names are A, B, C, D, and E, and one of them is to be chosen as the coordinator. Clearly any one out of them can be chosen so there are 5 ways. Now suppose two members are to be chosen for the position of coordinator and co-coordinator. Now, we can choose A as coordinator and one out of the rest 4 as co-coordinator. Similarly we can choose B as coordinator and one of out the remaining 4 as co-coordinator, and similarly with C, D and E. So there will be total 20 possible ways.

Combinatorial primitives

Let’s begin with a quick overview of the basic rules and objects that we will reference later.

The rule of sum

The rule of product

Let's generalize it. Permutations of choosing R disticnt objects out of a collection of N objects can be calculated using the following formula:

Combinations of choosing R distinct objects out of a collection of N objects can be calculated using the following formula:

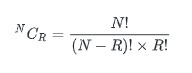
Basic Combinatorics Rules:

Suppose there are two sets A and B.

The basic rules of combinatorics one must remember are:

1. The Rule of Product:
   The product rule states that if there are X number of ways to choose one element from A and Y number of ways to choose one element from B, then there will be X*Y number of ways to choose two elements, one from A and one from B.
2. The Rule of Sum:
   The sum rule states that if there are X number of ways to choose one element from A and Y number of ways to choose one element from B, then there will be X+Y number of ways to choose one element that can belong to either A or to B.

These rules can be used for a finite collections of sets.

Permutations with repetition:

If we have N objects out of which N1 objects are of type 1,N2 objects are of type 2, ... Nk objects are of type k, then number of ways of arrangement of these N objects are given by:

Permutations without repetition:

When we choose k objects from n-element set in such a way that the order matters and each object can be chosen only once:

Combinations with repetition:

If we have N elements out of which we want to choose K elements and it is allowed to choose one element more than once, then number of ways are given by:

Combinations without repetition:

In combinations we choose a set of elements (rather than an arrangement, as in permutations) so the order doesn’t matter. The number of different k-element subsets (when each element can be chosen only once) of n-element set is:

In this blog we discussed about combinatorics, it focused mainly on the basic aspects and methods of counting. To learn more, I recommend you check out the reference works listed below, and keep practicing !!

References:

1. Hall M. "Combinatorial theory"
2. Cameron P.J. "Combinatorics: Topics, Techniques, Algorithms"
3. en.wikipedia.org :-)